class: center, top, title-slide .title[ # Statistical Inference ] .subtitle[ ## CRM Week 3 ] .author[ ### Charles Lanfear ] .date[ ### 29 Oct 2024<br>Updated: 30 Oct 2024 ] --- # Today * Regression and Models * Inferential Statistics * Hypothesis Testing * Theoretical Distributions * Properties of Means * Problems with Hypothesis Testing * Many wordy slides --- class: inverse # Regression  --- # Correlations Correlation ( `\(R\)` ) summarizes relationship between continuous variables -- `\(R\)` values: * Range from -1 to 1 * 0 indicates variables are *unrelated* * Can be squared to obtain **coefficient of determination**: `\(R^2\)` -- `\(R^2\)` indicates the *proportion* of variation in one variable **linearly** predicted by another -- `\(R^2\)` values: * Range from 0 to 1 * 0 indicates linearly unrelated * 1 indicates perfect linear relationship -- .text-center[ *A correlation of 0.5 between `\(x\)` and `\(y\)` indicates 25% of the variation in `\(y\)` is "explained" by `\(x\)` (and vice versa)* ] --- # Visualizing Correlations &nbsp; <!-- --> --- # Last Week's Correlation &nbsp; <!-- --> This is a strong relationship: About 66% of the variation is explained -- .pull-left[ But what is the *substantive* interpretation? ] -- .pull-right[ If pop density is 20, what do we expect crime to be? ] -- .text-center[ *What we want is a **model** to estimate how pop density predicts crime* ] --- class: inverse # Modeling  --- # The DGP When doing research, we're usually interested in saying something about how some part of the real world works -- The distributions of data we observe are the result of a real-world process we cannot directly observe -- We call this the **data generating process** (DGP) -- **Models** aim to approximate this data generating process mathematically to allow us to make quantitative statements about how the world works -- Most of the time, in any given project, we're really interested in an **estimate** of just one part of the DGP or one characteristic of the population * A distribution or measure of central tendency * A correlation or other association * A *causal effect*¹ .footnote[ More on this next week! ] --- # Estimation Going from observed data to some kind of estimate is a process involving three components: * **Estimand**: the real-world quantity we want to measure * **Estimate**: the measured quantity approximating our estimand * **Estimator**: the procedure we use to calculate the estimate using data -- Any given estimate consists also of three components: `$$Estimate = Estimand + Bias + Noise$$` -- **Noise** comes from *randomness* in the real world or sampling * We'll talk about this today -- **Bias** comes from *using the wrong estimator* * We'll mainly talk about this next week ---  .footnote[ Credit: [Richard McElreath](https://twitter.com/rlmcelreath/status/1582368904529137672) ] --- # Regression Regression is an estimation method for *fitting lines* to data -- Regression is just a way to summarize a relationship between variables using a line * e.g., predicting `\(Y\)` using `\(X\)` -- * The variable being predicted is the **dependent** or **outcome** variable * The variables used for prediction are **independent** or **explanatory** variables, sometimes called **covariates** or **regressors**¹ .footnote[[1] So many synonyms!] -- The regression line describes the **conditional expectation** of the dependent variable * e.g., the expected value (mean) of `\(Y\)` for different values of `\(X\)` --- # A Regression Line &nbsp; <!-- --> &nbsp; "If population density is 20, we expect the crime rate to be about 41" --- # Model Fitting The regression line represents an **estimate** of the association between population density and the crime rate (the estimand we want) -- The estimator used for **fitting** this line has two parts: 1. The model—this is the shape of the line (e.g., straight) and our choice of covariates 2. The estimation method—the maths to fit that shape to the data, e.g., **ordinary least squares** (OLS) -- OLS draws a line through the data that minimizes the *sum of squared residuals* * Residuals are the `\(Y\)` distances between the line and each point * OLS draws the line where the sum of squared residuals is *smallest* --- # Residuals &nbsp; <!-- --> .footnote[ [See here for an interactive explanation](https://setosa.io/ev/ordinary-least-squares-regression/) ] --- # Regression Equation Regression lines are defined by **parameters**: the **intercept** and **slope(s)** . -- Regression line equations look like this: `$$y_i = a + bx_i + e_i$$` -- `\(a\)` is the **intercept** * The expected value of `\(y\)` when `\(x = 0\)` -- `\(b\)` is a **slope** * The amount the expected value of `\(y\)` rises for every 1 unit increase in `\(x\)` -- `\(e_i\)` is the **residual** * The difference between prediction ( `\(a + bx\)` ) and *each value* of `\(y\)` * The square of this is what OLS is trying to minimize --- # Regression Equation &nbsp; <!-- --> --- # Predictions You can think of the regression line as being a set of predictions of `\(Y\)` for every value of `\(X\)` -- The regression formula—the intercept and coefficient(s)—tells us what those predictions are -- `$$CrimeRate = -20.8 + 3.09 PopDensity$$` We expect `\(CrimeRate\)` to be 3.09 higher for every additional unit of `\(PopDensity\)` When `\(PopDensity\)` is zero, the expected `\(CrimeRate\)` is `\(-20.8\)` -- If `\(PopDensity\)` is `\(20\)`, then we expect `\(CrimeRate\)` to be: `$$41 = -20.8 + 3.09*20$$` -- .text-center[ *The next question is whether this strong association likely holds in the population* ] --- class: inverse # Inferential Statistics <br> <br>  --- # Null Hypothesis Testing Recall that we want to learn about the true data generating process (DGP) -- We cannot observe it directly, but we can use data to infer things about it -- **Hypothesis testing** is one approach to learning about DGPs -- The basic idea: * Make an informed guess—a **hypothesis**—about what the DGP looks like * **Theory** is about DGPs! * Test if it is likely observed data were created by the hypothetical DGP * If it seems unlikely, we **reject** our hypothesis -- In short, we get closer to the truth by rejecting false explanations * *via negativa*: Knowledge by subtracting what is wrong --- # Significance Testing The simplest hypothesis testing is **null hypothesis significance testing** -- Process: 1. State hypotheses about estimand: * **Null Hypothesis**: There is no relationship * **Alternative Hypothesis**: There is a relationship -- 2. Make an estimate -- 3. Test how likely this estimate would be *if our null hypothesis is true* * This requires choosing a threshold for what we consider "unlikely" * e.g., less than 5% chance -- 4. Either reject or fail to reject the null; we do not *accept* the null -- .text-center[ *When we reject the null, we're confident our result is not just due to **noise*** ] --- # Frequentism Hypothesis testing is rooted in the **frequentist** paradigm of statistics -- Frequentism is based on the logic of *infinite* random sampling -- * For a given DGP, imagine randomly sampling from the population *forever* -- * The distribution of values in the samples (e.g., the means) would follow a known **theoretical distribution** * i.e., we know how likely it is to obtain any particular estimate *if the theoretical DGP is true* -- * Based on these theoretical distributions, we assess how (un)likely observed results are under a given hypothesis -- * Importantly, *all of these rely on properties of random sampling* * Non-random samples lead to **bias** --- class: inverse # Theoretical Distributions <br>  --- # Coin Flipping In theory, a normal coin is equally likely to land on heads or tails If we flipped it 20 times and got 13 heads, would we think it is a fair coin? -- What about 15 heads? -- If the coin is truly fair, it should have a 0.5 probability of coming up heads * Our null hypothesis is the coin is fair and has a heads probability of 0.5 * Our alternative is that it is *unfair*—likely to give either more or fewer heads than 0.5 -- We can calculate how likely it is to observe any particular number of heads flips if our null hypothesis is true * e.g., how likely is it to get 15 heads on 20 flips with a fair coin * We can do this just by tabulating every possible outcome of 20 coin flips --- # Ways to get... * There is only 1 way to get 0 heads: They're all tails! * There are 20 ways to get 1 head: Any 1 coin is heads! * There are 190 ways to get 2 heads * There are 4845 ways to 5 heads * There are *184,756* ways to get 10 heads! We're *1,000 times* more likely to get 10 heads than 2 heads! -- The probability we get any particular number of heads is can be described by a theoretical distribution: the **binomial distribution** --- # Binomial Distribution If we flip a fair coin 20 times, the binomial distribution says we're this likely to see each count of heads: <!-- --> Roughly 95% of the time, we'd expect to see between 6 and 14 heads. --- # p-values The **p-value** is the probability of observing a result at least as extreme as our estimate if the null hypothesis (a fair coin) were true. -- * The p-value for 15 out of 20 (75%) flips being heads is 0.041 * A fair coin would give us a result as far from 50% as this 1 in 25 times * p-values are typically calculated using a **test statistic** derived from a theoretical distribution (e.g., `\(t\)` or `\(\chi^2\)` tests) -- The *p-value* is *not* the probability our null hypothesis is true -- All a p-value tells us is how *frequently* the theoretical distribution we chose would generate the data we observe * p-values are only valid if we've chosen the right theoretical distribution -- Below `\(\alpha=.05\)` is often taken to indicate a "significant" p-value * That is, the point at which we are *confident* we can reject the null distribution as a source of our data --- # Errors `\(\alpha\)` is the rejection threshold, corresponding to a **confidence level** of `\(1-\alpha\)` * e.g., 95% confidence corresponds to `\(\alpha=.05\)` -- `\(\alpha\)` indicates our "comfort" in rejecting the null when it is *true* * e.g., `\(\alpha=.05\)` means we reject a true null 5% of the time -- Lower confidence levels lead to more **false positive** or **Type I error** * Rejecting the null when it is true -- Higher levels of confidence reduce false positives, but lead to more **false negatives** or **Type II errors** * Failing to reject the null when it is false -- .text-center[ *Choice of confidence levels is context-specific* ] --- # Cross-Tab Chi-Square We can test categorical associations using a chi-square ( `\(\chi^2\)` ) test. | |Area | | |:------------|:-----|:-----| |Disadvantage |Rural |Urban | |Low |63 |39 | |Medium |49 |48 | |High |41 |60 | Here we get a test statistic of 9.11 (df=2) corresponding to a statistically significant (at 95% confidence) p-value of 0.010. -- This suggests Disadvantage and Area are more strongly related in this sample than is likely to occur due only to sampling noise. * i.e. this is evidence for an association in the population --- class: inverse # Focusing on Means <br>  --- # Means When we want to infer something about the population from a sample, we often focus on some kind of mean -- This is because means have a useful sampling property, described by the **central limit theorem**: -- *No matter what the distribution of the variable in the population you sample from, the distribution of the **means** of all samples will be normally distributed around the population's mean*¹ .footnote[[1] Assuming at least a modest sample size and that the population distribution has a finite mean and variance---get out of here with your Cauchy-distributed variables!] -- &nbsp; .text-center[ *This sounds weird because it is weird* ] -- .text-center[ *It makes slightly more sense visually* ] --- # Illustration Imagine this is the distribution of a variable in the population <!-- --> The mean is in red, but the shape is definitely not a bell curve --- # One Sample Let's say we sample 100 observations from it and take the mean <!-- --> Our estimate isn't bad! But if we couldn't compare to the population, how would we know that? --- # Many Samples If we take a ton of samples (n=100 each) and calculate all their means, their distribution looks like this—most are pretty accurate! <!-- --> -- .text-center[ *Okay, sure, but what about **weird** distributions?* ] --- # wat Okay, look at this monster: <!-- --> There's barely any data near the mean at all! --- # Huh, okay This is the sampling distribution of the means we get from *that* <!-- --> .text-center[ *Yep, still works—just noisier!* ] --- # This is Nice Sample means being normally distributed around the population mean is *extremely useful* -- This means we can use the normal distribution (or something related to it) as a theoretical distribution in many different situations * Population Means * Differences in means * Correlations * Regression parameters * Categorical associations¹ .footnote[ *Kind of*—we can use the `\(\chi^2\)` which is based on the sum of squares of normal distributions ] -- In particular, we can use it to assess the precision and statistical significance of estimates --- # Standard Errors **Standard errors** measure the precision of our sample estimates -- Smaller standard errors indicate more precise estimates --  .footnote[Image credit: [Claus Wilke](https://clauswilke.com/dataviz/visualizing-uncertainty.html)] -- Larger sample sizes mean smaller standard errors --- # Confidence Intervals We can calculate confidence intervals from the standard error -- Intuitively, **confidence intervals** (CI) are a range of reasonably likely values for the estimand, given our observed sample values * Based on a **confidence level**, e.g. 95% * e.g., a 95% CI of (5.2, 7.5) is roughly compatible with estimands between 5.2 and 7.5 -- Less intuitively, if you re-estimated the quantity with new data infinitely, 95% of the 95% CIs would overlap the true estimand -- Confidence intervals are closely related to p-values: * The CI will not include zero if the p-value is significant * The CI will include zero when your p-value is not significant --- # Our Regression Here is a table of results from our regression earlier .text-85[ |Term |Estimate |Std Error |Statistic |P Value |Conf Low |Conf High | |:-----------|:--------|:---------|:---------|:-------|:--------|:---------| |Pop Density |3.09 |0.13 |23.54 |0.00 |2.84 |3.35 | |(Intercept) |-20.78 |2.09 |-9.94 |0.00 |-24.89 |-16.66 | ] This suggests a strong, statistically significant relationship between density and the crime rate -- Do we believe this is a good model, however? -- If for some reason we're only interested in the (unconditional, linear) association between density and the crime rate, this might be just fine! -- .text-center[ *Next week we'll get into estimates we might actually want to know* ] --- class: inverse # Hypothesis Testing Issues 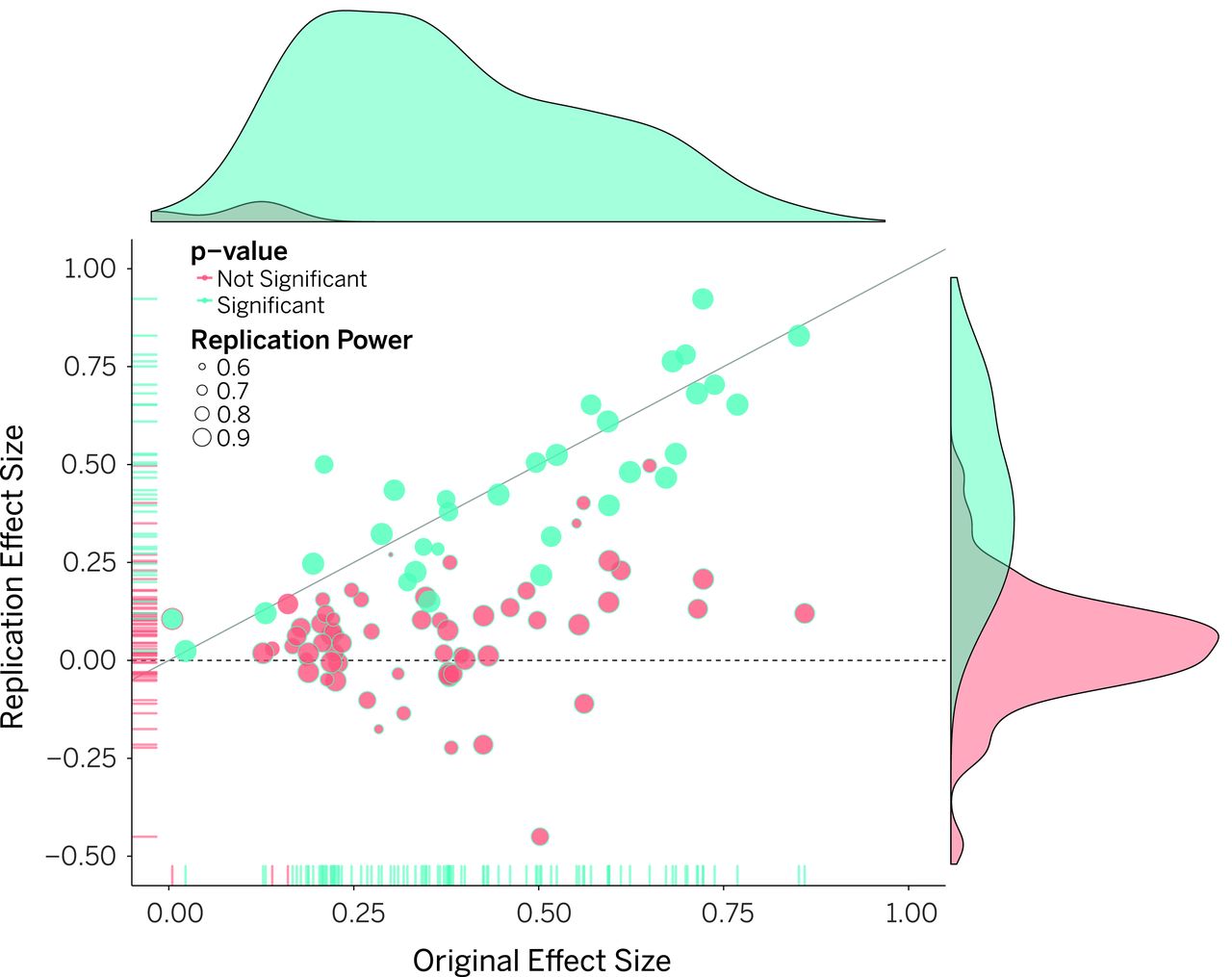 .footnote[ &zwj;Source: Open Science Collaboration (2015) "Estimating the reproducibility of psychological science" ] --- # Unethical Practices There are intense pressures on researchers to produce both high volume and high impact research -- It is trivial to perform many analyses, cherry-pick significant ones, then submit only those for review * The scientific community observes only what is submitted -- Similarly, one can invest enormous time and money into a project and receive null results * Inability to publish these is frustrating and damaging to careers --- # Screening Effects Due simply to random noise, even perfectly designed ethical research will routinely produce false positives at conventional confidence levels -- Journal peer reviewers and editors have historically declined submissions with null findings * Articles are rejected for being "not novel" * Articles are never submitted because authors know they will be rejected -- Conversely, these parties (and the media) often reward unexpected or "novel" significant results -- This leads to a number of problems: * Literatures filled with false positives * Literatures missing true negatives * Absence of replication studies (likely null findings) * Average estimates greater in magnitude than the real estimands --- # Responding The social sciences are slowly, begrudgingly moving to address these problems -- Some approaches: * Estimating publication bias * Pre-registration of analyses * Registered reports * Requirements for computational reproducibility * Replication studies * Publishing null findings -- These all work best to address researchers behaving *ethically* -- It can be *very hard* to detect unethical researchers * As is the case for many types of white-collar crime, it is mainly the incompetent who get caught --- ## Incompetent... but rich <br> .pull-left[  ] .pull-right[  ] --- class: inverse # Wrapping-Up Regression is just fancy line drawing * The line represents the conditional mean * We can use the line to make predictions -- Hypothesis tests are about comparing observed data and to theoretical distributions * Statistical significance means the observed data are unlikely to have come from the chosen theoretical distribution -- Be wary of the scientific literature * Constraints and incentives result in many false positives * Enforcement of research ethics is difficult --- class: inverse # Next Time Causality and Theory Testing! Your readings: * Huntington-Klein, N. (2022) *The Effect: An Introduction to Research Design and Causality*, New York, NY: Chapman and Hall/CRC Press. * Read pp. 87—128 & 144—159: (1) Chapter 6: Causal Diagrams, (2) Chapter 7: Drawing Causal Diagrams, (3) Chapter 8: Causal Paths and Closing Back Doors, (4) Chapter 10: Treatment Effects * Bueno de Mesquita, E. and Fowler, A. (2021) *Thinking Clearly with Data: A Guide to Quantitative Reasoning and Analysis*, Princeton, NJ: Princeton University Press. * Read pp. 193—242: (1) Chapter 9: Why Correlation Doesn’t Imply Causation, (2) Chapter 10: Controlling for Confounders, and (3) Chapter 11: Randomized Experiments